こんにちは!
今回は日々の授業についてのお話です✏️
アメリカのi2planningの生徒さんの授業です。
中学受験をする予定で今からたくさんの問題を解いて、合格に向けて頑張っています!
今回の授業では、倍数算を使った文章題をやりました。
このタイプの問題は
★差が一定→2人が同じ金額の品物を買っても2人の金額の差は一定。
2人の金額の比の差を買い物の前後で最小公倍数にして求める。
★和が一定→2人の間でお金のやり取りをしても2人の合計金額の和は一定。
2人の金額の比の和を、やりとりの前後で最小公倍数にして求める。
このどちらのパターンなのかで解き方が変わってきます。
例を見てみましょう。
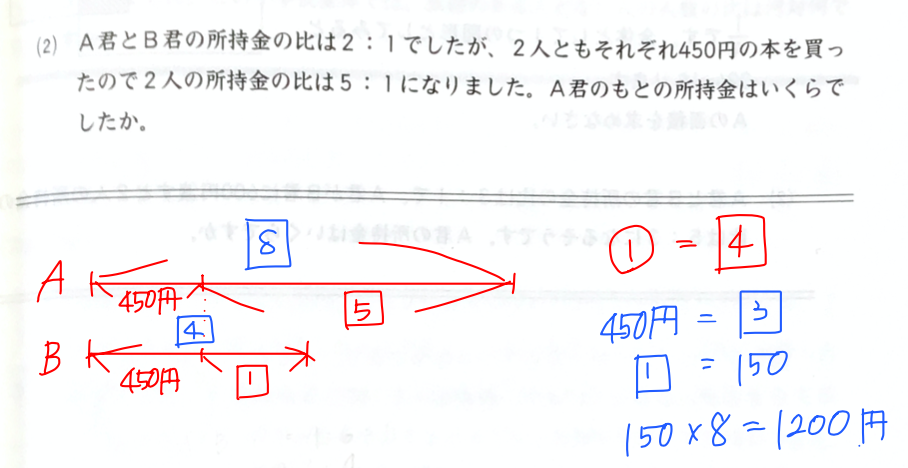
この問題は「差が一定」のパターンです。
2人とも同じ金額を払っているので、差は変わりません。
元々2:1の比が、払った後は5:1になりました。
この差を考えると、
払う前の比→2:1の2−1=①
払った後の比→5:1の5−1=❹
2人の差が一定なので、①=❹
となります。ですがこれでは比が揃っていないので、2:1=8:4となるように4倍して④=❹
として計算すると、450円=③にあたることがわかります。
ここまで来れば答えまでもう少しです。
①=150円となり、初めの兄が持っていた金額は⑧にあたるので
⑧=150×8=1200
答えは1200円です。
他の問題もそうですが、何を使ってどう解くのか、が分かれば答えまで辿り着けます。
算数や数学の授業では、その部分を自分で見つけられるように演習を重ねています!
何度もやっているうちに自分でも「この問題はこうすればいいんだ!」と分かるようになってきますよ😊
今回は小6算数についてでした!