こんにちは!
今日は雨で少し肌寒いですね☂️
今回は昨年度の授業から、中学3年生の図形の範囲から
相似比、面積比、体積比
の分野の問題です!
まず相似な図形とは?というところですが、私はよく
「ドラえもんのスモールライトやビッグライト」で表現します!
形は同じだけど大きさが違う、これが相似な図形です。
相似な図形ではどれだけの割合で大きいか小さいか、という相似比を求めますが
相似比が分かれば面積比や体積比もわかるんです!
面積はたて×横・底辺×高さ÷2・(上底+下底)×高さ÷2
など2つのものをかけて求めます。
だから単位も㎠と㎝の2乗になっている訳です。
相似比と面積比はこんな関係になっています↓
相似比 A:B
面積比 A2:B2
それと同じように考えると、
体積は底面積×高さ=たて×横×高さとなるので3つのものをかけて求めています。
単位は㎤で㎝の3乗となっています。よって相似比と体積比の関係はこうなります↓
相似比 A:B
体積比 A3:B3
これを頭に入れた上で問題を解いてみましょう。
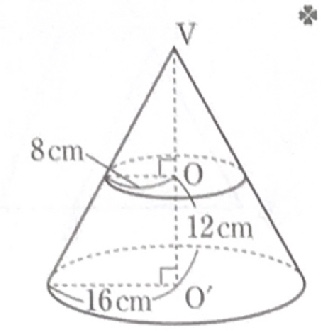
【問題】次の図で、円Oと円O’の面積比、円すいV-Oと円すい台O-O’の体積比をそれぞれ求めなさい。
まずは円Oと円O’の面積比!
これは円の半径の比が相似比になるので、
相似比 円O:円O’=1:2
面積比 円O:円O’=1:4
となります。
続いて体積比!
円すいOと円すい台O-O’は相似な形ではないので
相似なもの同士で体積比を求めてから円すい台の体積比を求めます。
相似なのは円すいOと円すいO’です。
相似比 円すいO:円すいO’=1:2
体積比 円すいO:円すいO’=1:8
円すい台O-O’=円すいO’–円すいO=8−1=7と計算できるので、
体積比 円すいO:円すい台O-O’=1:7
となります。
基本の比の形を活用すれば、少し変わった形でも対応することができますね!
できた時にはスッキリ〜!これが数学の楽しいところです🤗
一緒にスッキリ!味わいましょう〜🤘